作业 0922
返回 目录此页面提供 作业 0922 有关资料。
此作业的试题 PDF 提供于以下 链接 。
答案见下。
9/22 作业
Homework 4
-
(1) , , .
(2) , , 相同。
(3) .
-
, .
-
(a) .
(b) .
(c) .
(d) .
-
(a) because rank of the coefficient matrix is .
(b) Unique because is invertible.
(c) or .
since has unique solution.
or , then , and the system has either one or no solution.
-
(a) Infinitely many.
Because , has right inverse.
Therefore .
Lemma 1 , .
Proof
.
By lemma 1, obviously there are infinitely many right inverse of .
(b) Only .
Optional
-
a. is a solution.
b. .
c. .
d. .
-
a. .
b. .
c. Plot.
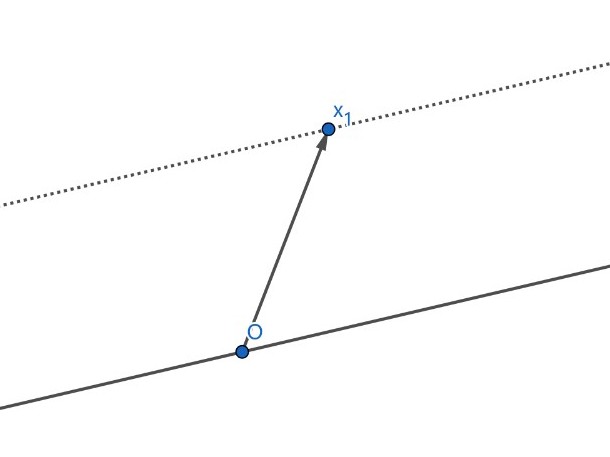
-
(1)(2) 证明
不妨令 是上三角矩阵。
, .
展开
如果 的主对角线均为 , 由于 是上三角矩阵
由于 , 不可能找到连续上升的 个下标 . 故至少一项 . 因此求和 (1) 的每一项均为 , , .
(3) 证明 .
Above Rendered from Markdown